Recently, the animation analysis technology is evolving rapidly. As one of its reasons, the improvement of the computer performance for processing the picture image data which is mass data can be mentioned. Now, animation photography is so familiar to us that mobile phones and smart phones are equipped standardly with the video function. A surveillance camera is most diffused as practical use of an animation. Especially the tendency is remarkable in urban areas in advanced nations. The main purpose of the surveillance camera is prevention of criminal acts, or their recording as the proof. As further advance, the future prediction of the animation photoed with the surveillance camera will be more effective for the prevention of the criminal acts.

In this research, the prediction technique of the future of the animation was developed by coupling the principal image extraction by Principal Component Analysis (PCA)^[1] and the time-series data prediction by the Singular Spectrum Analysis (SSA) ^[2,3].

An animation is constituted by many still images which interchange by a time series. A still image in a certain time step is set to I (t). Each I (t) is a 2-dimensional array of pixel values of the equal number to the pixel count of an image. In PCA, the images I(1)~ I(N) are rearranged into 1-dimensional arrays X (1) ~ X(N) and combined to a matrix Y (see Fig. 1). The eigen analysis of YYt, which is the autocorrelation matrix of Y, gives the eigen vectors Vi (i =1 ~ N) that correspond to the principal images of the movie.

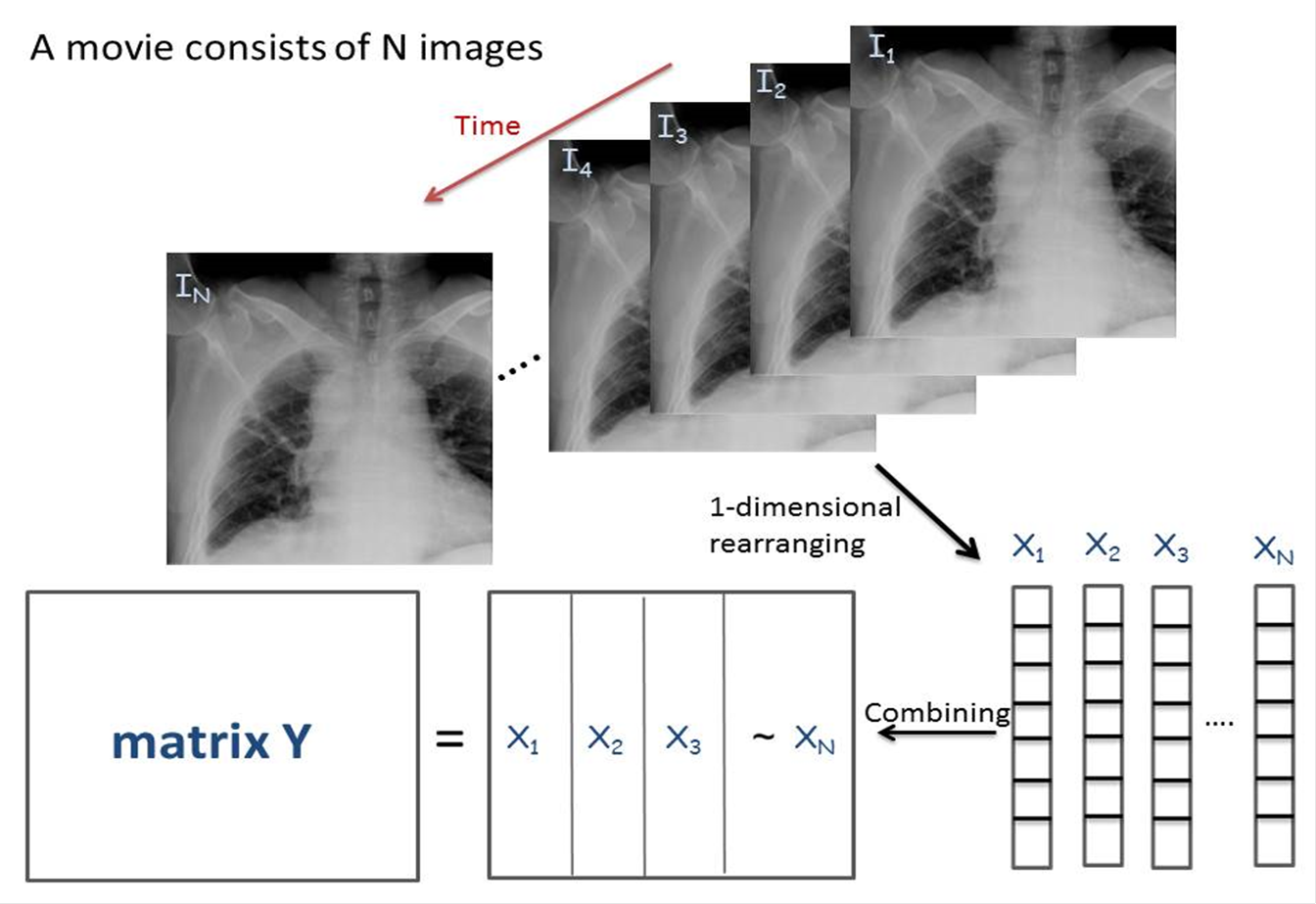
Fig.1 Combination of 1-dimentionaly rearranged N images of a movie

Here, we assumed that the I(t) can be separated to the time-dependent coefficients a_i(t) (i =1 ~ r, t = 1 ~ N) and the time-constant principle images V_i (i =1 ~ N) . Then, X(t) can be represented by eq. (1),

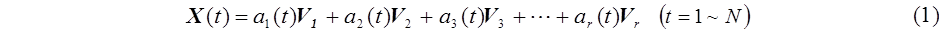
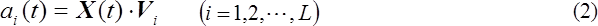
where L is a number smaller than N, and the condition of eigen vectors: 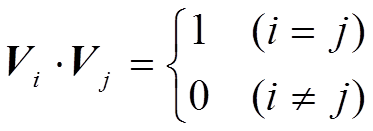is used for eq. (2) . If the future of time-dependent coefficients a_i(t) (i =1 ~ L, t = 1 ~ N) can be predicted, its substitution to eq. (1) makes the predicted future of the movie : I(N+k) (k=1,2,3,…).

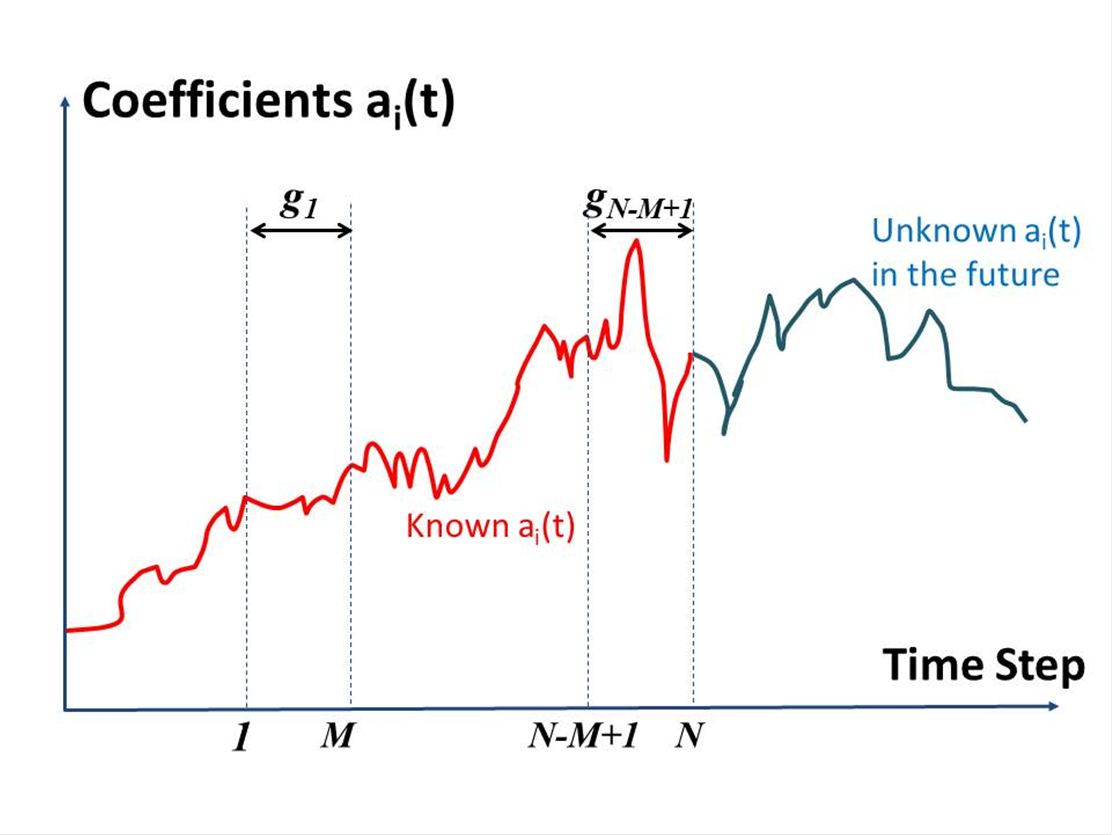
Fig.2 Known and predicted coefficients a(t)

The Singular Spectrum Analysis (SSA) was used to predict the future of the time-series data a_i(t) (i =1 ~ L, t = 1 ~ N). In SSA, as shown in Fig. 2, the vectors gi,1, gi,2, …, gi,N-M+1 are derived from the known a_i(t) as,

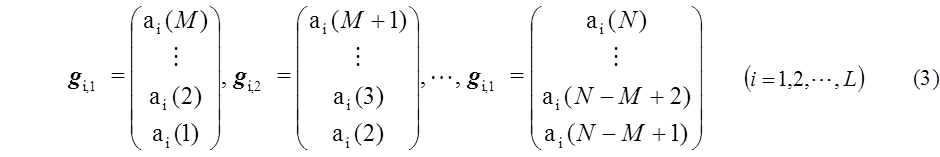
The eigen vectors u_i,k of the autocorrelation matrix ZZ^T, where Z = [gi,1 gi,2 … gi,N-M+1] for each i are the R eigen vectors u₁, … , u_R of the largest R eigen values are arranged horizontally as

The predicted coefficient aⁱ(N+1) at the future time step t = N+1 can be obtained as the first component of the vector gi,N-M+2 which satisfies the following equation (4),

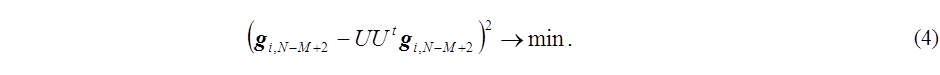
By repeating the above calculation, the coefficients a_i(N+2), a_i(N+3), a_i(N+4), … can be calculated to make the future of the movie : I(N+1), I(N+2), I(N+3), I(N+4), … .

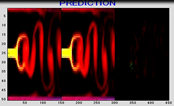
Fig. 3 shows the prediction simulation result of the animation by the Karman’s vortex calculation. The left is the original animation, the center is the prediction simulation result, and the right is the error of them. Little error were seen and it was shown that the animation prediction by this technique can be carrying out with sufficient accuracy.
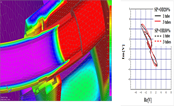
Fig. 4 shows the prediction simulation result of a hand opening and closing. Little error is seen like prediction of the Karman’s vortex animation. Thus, the animation’s future prediction was succeeded with this technique also about the photoed animation.

This technique is expected for various applications, such as the criminal prevention with the surveillance camera, and the accident prevention with the in-vehicle camera. From now on, improvement of this technique will be continued aiming at the further accuracy improvement and the expansion of applicable fields.

1. (1) Components: Every visible component

1. (2) Location: Anywhere

1. (3) Material: Anything

1. (4) Condition: In the atmosphere

1. (1)A new technique was developed to predict future of animation

1. (2)The Principal Component Analysis (PCA) is applied for the extraction of principle images of the animation.

1. (3)The Singular Spectrum Analysis (SSA) was applied for the prediction of the time-series data prediction.

1. [1]M. Turk and A. Pentland, “Eigenfaces for Recognition”, Journal of Cognitive Neuro- science, Vol.3, NO.1, pp.71-86,(1991)
2. [2]R. Vartard and M. Ghil,”Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series,” Physica D, 35, pp.395-424,(1989).
3. [3]M. Ghil, M. R. Allen, M. D. Dettinger, K. Ide, D. Kondrashov, M. E. Mann, et al., "Advanced spectral methods for climatic time series," Reviews of Geophysics, vol. 40, Aug-Sep 2002.

Japan Society of Maintenology (ejam@jsm.or.jp)